前言
求弦长问题,常见于直线和圆,直线和椭圆,直线和双曲线,直线和抛物线相交所形成的弦的长度问题。
常用公式:
A、直角坐标系下,针对直线和曲线的普通方程,\(|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|\),
B、直角坐标系下,针对直线的参数方程和曲线的普通方程,\(|AB|=|t_1-t_2|\),
C、极坐标系下,针对过极点的直线和曲线的极坐标方程,\(|AB|=|\rho_A-\rho_B|\)
直线和圆的弦长
常用方法:
①几何方法;利用弦心距、半弦长、半径所形成的\(Rt\Delta\)求解,还用到点到直线的距离公式。
②弦长公式;\(|AB|=\sqrt{1+k^2}|x_1-x_2|\),运算量稍大一些;
③直线的参数方程法;\(|AB|=|t_1-t_2|\),此时需要注意直线的参数方程必须是标准形式,这种方法不太好理解。
其中以几何方法最为简单。举例如下,
例1【2019届凤中高三理科月考1第22题】
在平面直角坐标系\(xoy\)中,直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=2+t}\\{y=1+2t}\end{array}\right.(t为参数)\),以原点为极点,以\(x\)轴的非负半轴为极轴建立极坐标系,\(\odot C\)的极坐标方程为\(\rho^2-4\rho sin\theta-12=0\),
(1) 求\(\odot C\)的参数方程;
分析:将\(\rho^2=x^2+y^2\),\(y=\rho\cdot sin\theta\)
代入\(\odot C\)的极坐标方程\(\rho^2-4\rho sin\theta-12=0\),
得到\(\odot C\)的直角坐标方程为\(x^2+y^2-4y-12=0\),
即\(x^2+(y-2)^2=16=4^2\),
故\(\odot C\)的参数方程为\(\left\{\begin{array}{l}{x=4cos\theta}\\{y=2+4sin\theta}\end{array}\right.\) (\(\theta\)为参数,\(\theta\in [0,2\pi)\))。
(2)求直线\(l\)被\(\odot C\)截得的弦长。
【法1,几何方法,\(Rt\Delta\)】将直线\(l\)的参数方程消参,得到其普通方程为\(2x-y-3=0\),
则圆心\((0,2)\)到直线的距离为\(d=\cfrac{|-2-3|}{\sqrt{2^2+1^2}}=\sqrt{5}\),
则直线\(l\)被\(\odot C\)截得的弦长为\(2\sqrt{r^2-d^2}=2\sqrt{4^2-(\sqrt{5})^2}=2\sqrt{11}\)。
【法2,弦长公式】设直线和圆的交点为\(A(x_1,y_1),B(x_2,y_2)\),
联立得到方程组,\(\left\{\begin{array}{l}{2x-y-3=0}\\{x^2+y^2-4y-12=0}\end{array}\right.\)
消去\(y\)得到,\(x^2+(2x-3)^2-4(2x-3)-12=0\),
整理得到,\(5x^2-20x+9=0\),
由韦达定理得到,\(x_1+x_2=4\),\(x_1x_2=\cfrac{9}{5}\),
由弦长公式得到,\(|AB|=\sqrt{1+k^2}|x_1-x_2|\)
\(=\sqrt{1+2^2}\sqrt{(x_1+x_2)^2-4x_1x_2}\)
\(=\sqrt{5}\sqrt{16-\cfrac{36}{5}}=2\sqrt{11}\)。
【法3,利用直线的参数方程求解】
直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=2+t}\\{y=1+2t}\end{array}\right.(t为参数)\),
(此时千万要注意,弦长\(|AB|\neq |t_1-t_2|\),原因是这个参数方程不是标准形式的)
将其做如下的转化,
\(\left\{\begin{array}{l}{x=2+\cfrac{1}{\sqrt{5}}\cdot \sqrt{5}t}\\{y=1+\cfrac{2}{\sqrt{5}}\cdot \sqrt{5}t}\end{array}\right.(t为参数)\),
令\(\sqrt{5}t=m\),则其参数方程的标准形式为
\(\left\{\begin{array}{l}{x=2+\cfrac{1}{\sqrt{5}}\cdot m}\\{y=1+\cfrac{2}{\sqrt{5}}\cdot m}\end{array}\right.(m为参数)\),
【此时参数\(m\)的几何意义才是动点到静点的距离的数量,千万要注意,即弦长\(|AB|=|m_1-m_2|\)】
将直线\(l\)的参数方程的标准形式代入圆的普通方程得到,
\((2+\cfrac{1}{\sqrt{5}}m)^2+(1+\cfrac{2}{\sqrt{5}}m)^2-4(1+\cfrac{2}{\sqrt{5}}m)-12=0\)
整理为\(m^2-11=0\),
令直线和圆的两个交点\(A,B\)分别对应的参数为\(m_1,m_2\),
则\(m_1+m_2=0\),\(m_1m_2=-11\),
此时弦长\(|AB|=|m_1-m_2|=\sqrt{(m_1+m_2)^2-4m_1m_2}=\sqrt{4\times 11}=2\sqrt{11}\)。
- 以下方法都需要用到直线的参数方程,故需要学会如何将一个直线的普通方程转化为参数方程。
如给定直线\(y=2x+1\),其中点\((0,1)\),点\((1,3)\)都在其上,
我们现在想求做过点\((1,3)\)的直线\(y=2x+1\)的参数方程,
可以这样做,依照模板\(\left\{\begin{array}{l}{x=x_0+cos\theta \cdot t}\\{y=y_0+sin\theta\cdot t}\end{array}\right.(t为参数)\)
定点坐标为\((x_0,y_0)=(1,3)\),
可知\(k=tan\theta=2\),引入非零比例因子\(k\),
得到\(sin\theta=2k\),\(cos\theta=k(k>0)\),
由\(sin^2\theta+cos^2\theta=1\),得到\(k=\cfrac{\sqrt{5}}{5}\),
则可知\(cos\theta=\cfrac{\sqrt{5}}{5}\),\(sin\theta=\cfrac{2\sqrt{5}}{5}\)
故所给定直线\(y=2x+1\)的参数方程为
\(\left\{\begin{array}{l}{x=1+\cfrac{\sqrt{5}}{5} t}\\{y=3+\cfrac{2\sqrt{5}}{5} t}\end{array}\right.(t为参数)\)
总结思路:①找个定点;②求解\(cos\theta\)和\(sin\theta\);③带入模板,OK!
直线和椭圆的弦长
常用方法:
①几何方法不再适用;
②弦长公式还能使用;\(|AB|=\sqrt{1+k^2}|x_1-x_2|\),运算量稍大一些;
③直线的参数方程法;\(|AB|=|t_1-t_2|\),需要注意直线的参数方程必须是标准形式;
其中以直线的参数方程法最为简单。举例如下,
直线和双曲线的弦长
常用方法:
①几何方法不再适用;
②弦长公式还能使用;\(|AB|=\sqrt{1+k^2}|x_1-x_2|\),运算量稍大一些;
③直线的参数方程法;\(|AB|=|t_1-t_2|\),需要注意直线的参数方程必须是标准形式;
其中以直线的参数方程法最为简单。举例如下,
直线和抛物线的弦长
常用方法:
①几何方法不再适用;
②弦长公式还能使用;\(|AB|=\sqrt{1+k^2}|x_1-x_2|\),运算量稍大一些;
③直线的参数方程法;\(|AB|=|t_1-t_2|\),需要注意直线的参数方程必须是标准形式;
其中以直线的参数方程法最为简单。
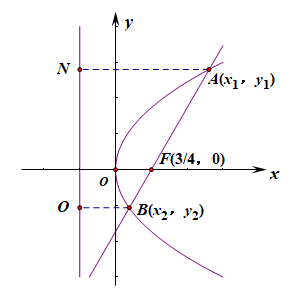
例2设抛物线\(C:y^2=3x\)的焦点,过F且倾斜角为\(30^{\circ}\)的直线交C于A,B两点,则\(|AB|\)等于()
【法1】:常规方法,利用两点间距离公式,由于\(2p=3\),则\(\cfrac{p}{2}=\cfrac{3}{4}\),故焦点\(F(\cfrac{3}{4},0)\),又斜率为\(k=\cfrac{\sqrt{3}}{3}\),
则直线\(AB\)的方程为\(y=\cfrac{\sqrt{3}}{3}(x-\cfrac{3}{4})\),
联立直线\(AB\)和抛物线方程,得到\(\left\{\begin{array}{l}{y^2=3x}\\{y=\cfrac{\sqrt{3}}{3}(x-\cfrac{3}{4})}\end{array}\right.\),
消\(y\)得到\(16x^2-24\times7x+9=0\),设点\(A(x_1,y_1)\),点\(B(x_2,y_2)\),
则\(x_1+x_2=\cfrac{24\times7}{16}=\cfrac{21}{2}\),\(x_1x_2=\cfrac{9}{16}\),
故\(|AB|=\sqrt{1+k^2}\cdot |x_1-x_2|\)
\(=\sqrt{1+k^2}\cdot\sqrt{(x_1+x_2)^2-4x_1x_2}=12\)。
【法2】:利用直线\(AB\)的参数方程的参数的几何意义,
直线\(AB\)的参数方程为\(\begin{cases}x=\cfrac{3}{4}+\cfrac{\sqrt{3}}{2}t\\y=0+\cfrac{1}{2}t\end{cases}(t为参数)\),将其代入\(y^2=3x\)中,
整理得到\(t^2-6\sqrt{3}t-9=0\),设\(A\),\(B\)对应的参数分别为\(t_1\),\(t_2\),
则\(\Delta>0\),且有\(t_1+t_2=6\sqrt{3}\),\(t_1t_2=-9\),
故\(|AB|=|t_1-t_2|=\sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{36\times3-4\times(-9)}=12\)。
【法3】:利用抛物线的定义可知,\(|AB|=|AF|+|BF|=|AN|+|BO|=x_1+\cfrac{p}{2}+x_2+\cfrac{p}{2}=x_1+x_2+p\),

故由法1中,得到\(x_1+x_2=\cfrac{24\times7}{16}=\cfrac{21}{2}\),\(p=\cfrac{3}{2}\),即\(|AB|=x_1+x_2+p=12\)。
法4:利用抛物线的焦点弦长公式:\(|AB|=\cfrac{2p}{sin^2\alpha}\),
则\(|AB|=\cfrac{2\times \cfrac{3}{2}}{(\cfrac{1}{2})^2}=12\)。
典例剖析
例7【2019届理科数学周末训练1第22题】
已知直线\(l\)的极坐标方程为\(\rho sin(\theta-\cfrac{\pi}{3})=0\),以极点为平面直角坐标系的原点,极轴为\(x\)轴的正半轴,建立平面直角坐标系,
曲线\(C\)的参数方程为\(\left\{\begin{array}{l}{x=2cos\alpha}\\{y=2+2sin\alpha}\end{array}\right.(\alpha为参数)\)。
(1)求直线\(l\)被曲线\(C\)截得的弦长|OA|。
分析:可以从以下四个角度思考,
①利用两点间的距离公式;
【法1】直线\(l\)的普通方程为\(y=\sqrt{3}x\),圆\(C\)的普通方程为\(x^2+(y-2)^2=2^2\),
联立消掉\(y\),得到\(x^2-\sqrt{3}x=0\),
解得,\(\left\{\begin{array}{l}{x_1=0}\\{y_1=0}\end{array}\right.\),或\(\left\{\begin{array}{l}{x_2=\sqrt{3}}\\{y_2=3}\end{array}\right.\),
由两点间距离公式得到\(|OA|=2\sqrt{3}\)。
②直线和圆相交求弦长的几何方法;
【法2】直线为\(\sqrt{3}x-y=0\),圆心为\((0,2)\),
则圆心到直线的距离为\(d=\cfrac{|0-2|}{2}=1\),又半径为\(2\),
故半弦长为\(\sqrt{2^2-1^2}=\sqrt{3}\),则弦长\(|OA|=2\sqrt{3}\)。
③直线的参数方程法;
【法3】由于直线的普通方程为\(y=\sqrt{3}x\),经过点\((0,0)\),
斜率\(k=tan\theta=\sqrt{3}\),
直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=0+\cfrac{1}{2}t}\\{y=0+\cfrac{\sqrt{3}}{2}t}\end{array}\right.(t为参数)\),
将其代入圆的普通方程\(x^2+(y-2)^2=2^2\),
整理得到\(t^2-2\sqrt{3}t=0\),
解得\(t_1=0\),\(t_2=2\sqrt{3}\),
则弦长\(|OA|=|t_1-t_2|=2\sqrt{3}\)。
④极坐标法;
【法4】直线的极坐标方程为\(\theta=\cfrac{\pi}{3}\),
圆的极坐标方程为\(\rho=4sin\theta\),
二者联立,得到\(\rho=4sin\cfrac{\pi}{3}=2\sqrt{3}\)。
即所求弦长\(|OA|=2\sqrt{3}\)。
(2)从极点做曲线\(C\)的弦,求弦的中点\(M\)轨迹的极坐标方程。
分析:可以从以下三个角度思考:
①利用平面直角坐标系下的中点公式;
【法1】相关点法,在平面直角坐标系中,设过坐标原点的直线和圆相交于点\(P(x_0,y_0)\),则所得弦的中点坐标为\(M(x,y)\)
则\(\left\{\begin{array}{l}{2x=x_0}\\{2y=y_0}\end{array}\right.\),又点\(P(x_0,y_0)\)在圆\(x^2+(y-2)^2=2^2\)上,
代入整理得到普通方程为\(x^2+(y-1)^2=1\),
即其极坐标方程为\(\rho=2sin\theta\),
其中\(\alpha\in(0,\pi)\),而不是\(\alpha\in[0,\pi)\),以保证弦的存在。
②利用圆的参数方程;
由于圆上任意一动点\(P\)的坐标\(P(2cos\theta,2+2sin\theta)\),则弦的中点\(M(cos\theta,1+sin\theta)\),
即点\(M\)的参数方程为\(\left\{\begin{array}{l}{x=cos\theta}\\{y=1+sin\theta}\end{array}\right.(\theta为参数)\),
消去参数\(\theta\),得到普通方程为\(x^2+(y-1)^2=1\),
即其极坐标方程为\(\rho=2sin\theta\),
其中\(\alpha\in(0,\pi)\),而不是\(\alpha\in[0,\pi)\),以保证弦的存在。
③利用极坐标法;
【法3】曲线\(C\)的极坐标方程为\(\rho=4sin\theta\),
过极点的直线的极坐标方程为\(\theta=\alpha\),
设直线和曲线\(C\)的交点的极坐标为\((\rho_1,\alpha)\),
则弦的中点\(M\)的极坐标为\((\rho,\alpha)\),
由题目可知,\(\rho_1=2\rho\),代入曲线\(C\)的极坐标方程为\(2\rho=4sin\alpha\),
得到\(\rho=2sin\alpha\),其中\(\alpha\in(0,\pi)\)。
故弦的中点\(M\)轨迹的极坐标方程为\(\rho=2sin\alpha\),其中\(\alpha\in(0,\pi)\)。
说明:由于弦的中点要存在,则必须保证\(\rho\neq 0\),即原来的\(\alpha\in[0,\pi)\),必须变为\(\alpha\in(0,\pi)\)。
对应练习
练1已知点\(M\)在圆\(C:x^2+y^2-4y+3=0\)上,点\(N\)在曲线\(y=1+lnx\)上,则线段\(MN\)的长度的最小值为_______。
提示:曲线\(y=1+lnx\)的切线为\(y=x\),则原问题转化为点\((cos\theta,2+sin\theta)\)到直线\(x-y=0\)的点线距。\(d_{min}=\sqrt{2}-1\)。